Cardinalidade, em banco de dados, está ligado as relações entre suas tabelas e quantos dados de uma entidade (tabela) estão presentes na outra entidade.
Da matemática o conceito de cardinalidade, de modo simples, vem de elementos de um determinado conjunto que estão em outro conjunto.
Exemplo:
Dados os conjuntos A = {1,2,3,4,5} e B = {1,3,5}
Podemos afirmar que o conjunto de B é um subconjunto de A. Podemos afirmar também que B está contido em A ou que A contém B. Podemos assim concluir que A e B tem uma relação.
Se você entendeu esse conceito, imagine agora um banco de dados com esses conjuntos A e B, sendo eles entidades (tabelas) do banco de dados e seus números A = {1,2,3,4,5} e B = {1,3,5} são considerados como os atributos do banco de dados.
Simplificando ainda mais:
Ao invés de A vamos substituir por um conjunto chamado Clientes e ao invés de {1,2,3,4,5} vamos usar os atributos {Código,Nome,Sobrenome,Idade,CPF}.
Agora da mesma forma substituiremos B pela entidade Identificação_Clientes e seus atributos serão derivados de Clientes, sendo: {Código,Sobrenome,CPF}
Nesse exemplo temos a entidade Identificação_Clientes sendo derivada de atributos da entidade Clientes.
Na matemática esses conjuntos A = {1,2,3,4,5} e B = {1,3,5} são considerados como uma Função Injetora, pois todos os elementos de B (domínio) se relacionam com um elemento de A (contra domínio).
Na matemática temos 3 tipos de função:
Função Injetora: todos os elementos do domínio se relacionam com apenas um elemento do contra domínio, podendo sobrar elementos no domínio.
Função Sobrejetora: todos os elementos do contra domínio se relacionam a um elemento do domínio.
Função Bijetora: a função é ao mesmo tempo injetora e sobrejetora. Ou seja, tem a quantidade de elementos iguais e todos se relacionam.
Tipos de relacionamento
Ao criar um relacionamento entre tabelas de um banco de dados podemos utilizar das cardinalidades:
1:1: um-para-um; o mais simples do relacionamentos o relacionamento de A para B permite apenas 1 valor de A para 1 de B.
1:N: um-para-muitos; 1 valor de A se relaciona com muitos de B.
N:1: muitos-para-um; muitos valores de A se relacionam com 1 de B. Observe que apenas mudamos o ponto de vista. a relação é a mesma da anterior.
Obs.: na cardinalidade 1:N e N:1 a chave primária (Primary Key) da entidade é levada do UM para o N. Observe as setas. (Se você não sabe oque é uma chave primária, entre aqui).
N:N: muitos-para-muitos; muitos valores de A se relacionam com muitos de B. Neste caso há a necessidade do uso de outra entidade (tabela), chamamos isso de entidade associativa.
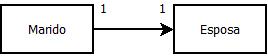


Nenhum comentário:
Postar um comentário